Sfoglia il codice sorgente
Wetere Fragen Vektorgeometrie
11 ha cambiato i file con 57 aggiunte e 111 eliminazioni
+ 4
- 0
.gitignore
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 1 | 5 |
|
| 2 | 6 |
|
| 3 | 7 |
|
+ 3
- 2
21_22_A/6MT19c_pr1_VECG1/Pruefung.tex
Vedi File
|
||
| 30 | 30 |
|
| 31 | 31 |
|
| 32 | 32 |
|
| 33 |
|
|
| 33 |
|
|
| 34 | 34 |
|
| 35 | 35 |
|
| 36 | 36 |
|
| 37 |
|
|
| 37 | 38 |
|
| 38 |
|
|
| 39 |
|
|
| 39 | 40 |
|
| 40 | 41 |
|
| 41 | 42 |
|
+ 0
- 12
aufgaben/P_TALS/vecg1/AdditionSubtraktion_v1.tex~
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
+ 31
- 0
aufgaben/P_TALS/vecg1/DreiKraefte_v1.tex
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
+ 0
- 12
aufgaben/P_TALS/vecg1/Gegenvektor_v1.tex~
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
+ 0
- 15
aufgaben/P_TALS/vecg1/Linearkombination_v1.tex~
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
+ 0
- 9
aufgaben/P_TALS/vecg1/Parallelogramm_v1.tex~
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
+ 19
- 0
aufgaben/P_TALS/vecg1/PolarkoordinatenUmrechnen_v1.tex
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
+ 0
- 12
aufgaben/P_TALS/vecg1/Repraesentant_v1.tex~
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
+ 0
- 49
aufgaben/P_TALS/vecg1/Vereinfachen_v1.tex~
Vedi File
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 36 |
|
|
| 37 |
|
|
| 38 |
|
|
| 39 |
|
|
| 40 |
|
|
| 41 |
|
|
| 42 |
|
|
| 43 |
|
|
| 44 |
|
|
| 45 |
|
|
| 46 |
|
|
| 47 |
|
|
| 48 |
|
|
| 49 |
|
|
BIN
aufgaben/P_TALS/vecg1/img/DreiKraefte.jpg
Vedi File
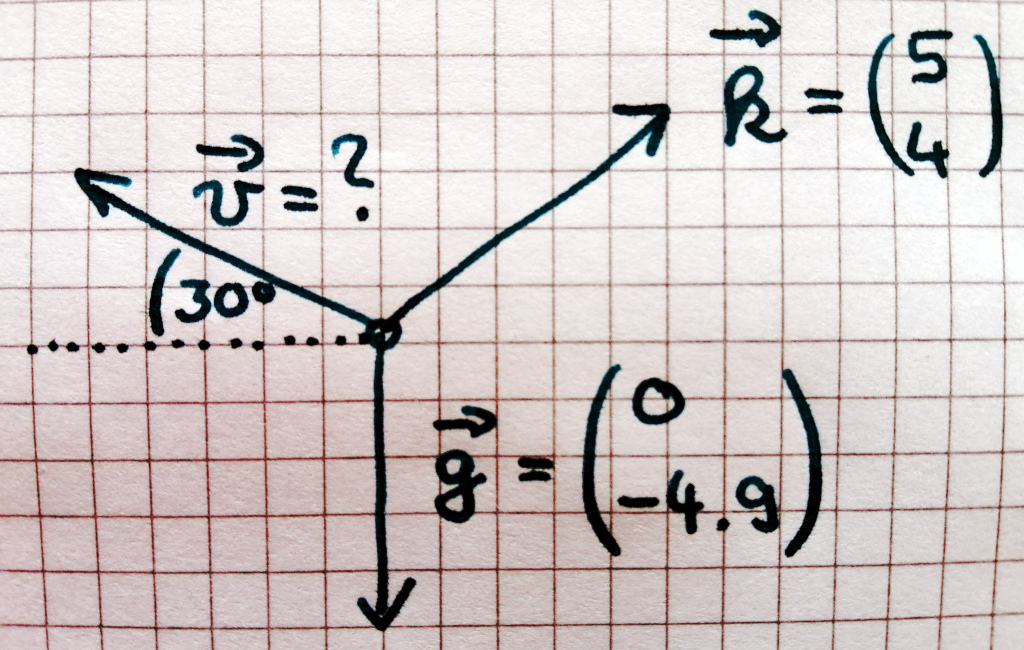
Loading…
