Przeglądaj źródła
Merge branch 'master' of http://gitea.freimann.eu:3001/phi/Pruefungen
48 zmienionych plików z 685 dodań i 38 usunięć
+ 0
- 19
20_21_B/6MT19f_pr3_BeruehrendeGraphen/Lernziele.txt
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
+ 1
- 0
20_21_B/6MT19g_pr1_Quadratische_Funktionen_Nachpruefung/.gitignore
Wyświetl plik
|
||
| 1 |
|
|
20_21_B/6MT19c_pr2_BeruehrendeGraphen/Lernziele.txt → 20_21_B/6MT19g_pr1_Quadratische_Funktionen_Nachpruefung/Lernziele.txt
Wyświetl plik
+ 76
- 0
20_21_B/6MT19g_pr1_Quadratische_Funktionen_Nachpruefung/Pruefung.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 36 |
|
|
| 37 |
|
|
| 38 |
|
|
| 39 |
|
|
| 40 |
|
|
| 41 |
|
|
| 42 |
|
|
| 43 |
|
|
| 44 |
|
|
| 45 |
|
|
| 46 |
|
|
| 47 |
|
|
| 48 |
|
|
| 49 |
|
|
| 50 |
|
|
| 51 |
|
|
| 52 |
|
|
| 53 |
|
|
| 54 |
|
|
| 55 |
|
|
| 56 |
|
|
| 57 |
|
|
| 58 |
|
|
| 59 |
|
|
| 60 |
|
|
| 61 |
|
|
| 62 |
|
|
| 63 |
|
|
| 64 |
|
|
| 65 |
|
|
| 66 |
|
|
| 67 |
|
|
| 68 |
|
|
| 69 |
|
|
| 70 |
|
|
| 71 |
|
|
| 72 |
|
|
| 73 |
|
|
| 74 |
|
|
| 75 |
|
|
| 76 |
|
|
+ 0
- 0
20_21_B/6MT19g_pr1_Quadratische_Funktionen_Nachpruefung/TALS.flag
Wyświetl plik
+ 1
- 0
20_21_B/6MT19g_pr1_Quadratische_Funktionen_Nachpruefung/clean.sh
Wyświetl plik
|
||
| 1 |
|
|
+ 1
- 0
20_21_B/6MT19g_pr1_Quadratische_Funktionen_Nachpruefung/makeBoth.sh
Wyświetl plik
|
||
| 1 |
|
|
+ 0
- 19
20_21_B/6MT19g_pr3_BeruehrendeGraphen/Lernziele.txt
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
+ 1
- 0
20_21_B/6MT19i_pr2_Quadratische_Funktionen_Nachpruefung/.gitignore
Wyświetl plik
|
||
| 1 |
|
|
+ 72
- 0
20_21_B/6MT19i_pr2_Quadratische_Funktionen_Nachpruefung/Pruefung.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 36 |
|
|
| 37 |
|
|
| 38 |
|
|
| 39 |
|
|
| 40 |
|
|
| 41 |
|
|
| 42 |
|
|
| 43 |
|
|
| 44 |
|
|
| 45 |
|
|
| 46 |
|
|
| 47 |
|
|
| 48 |
|
|
| 49 |
|
|
| 50 |
|
|
| 51 |
|
|
| 52 |
|
|
| 53 |
|
|
| 54 |
|
|
| 55 |
|
|
| 56 |
|
|
| 57 |
|
|
| 58 |
|
|
| 59 |
|
|
| 60 |
|
|
| 61 |
|
|
| 62 |
|
|
| 63 |
|
|
| 64 |
|
|
| 65 |
|
|
| 66 |
|
|
| 67 |
|
|
| 68 |
|
|
| 69 |
|
|
| 70 |
|
|
| 71 |
|
|
| 72 |
|
|
+ 0
- 0
20_21_B/6MT19i_pr2_Quadratische_Funktionen_Nachpruefung/TALS.flag
Wyświetl plik
+ 1
- 0
20_21_B/6MT19i_pr2_Quadratische_Funktionen_Nachpruefung/clean.sh
Wyświetl plik
|
||
| 1 |
|
|
+ 1
- 0
20_21_B/6MT19i_pr2_Quadratische_Funktionen_Nachpruefung/makeBoth.sh
Wyświetl plik
|
||
| 1 |
|
|
+ 1
- 0
20_21_B/6VG20r_pr3_ExpFct_und_Datenanalyse/.gitignore
Wyświetl plik
|
||
| 1 |
|
|
+ 0
- 0
20_21_B/6VG20r_pr3_ExpFct_und_Datenanalyse/GESO.flag
Wyświetl plik
+ 14
- 0
20_21_B/6VG20r_pr3_ExpFct_und_Datenanalyse/Lernziele.txt
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
+ 29
- 0
20_21_B/6VG20r_pr3_ExpFct_und_Datenanalyse/Pruefung.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
+ 1
- 0
20_21_B/6VG20r_pr3_ExpFct_und_Datenanalyse/clean.sh
Wyświetl plik
|
||
| 1 |
|
|
+ 1
- 0
20_21_B/6VG20r_pr3_ExpFct_und_Datenanalyse/makeBoth.sh
Wyświetl plik
|
||
| 1 |
|
|
+ 37
- 0
pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/saettigung/Benzylpenicilin_v1.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 36 |
|
|
| 37 |
|
|
+ 47
- 0
pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/saettigung/Benzylpenicilin_v1.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 36 |
|
|
| 37 |
|
|
| 38 |
|
|
| 39 |
|
|
| 40 |
|
|
| 41 |
|
|
| 42 |
|
|
| 43 |
|
|
| 44 |
|
|
| 45 |
|
|
| 46 |
|
|
| 47 |
|
|
+ 47
- 0
pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/saettigung/Pizza_v1.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 36 |
|
|
| 37 |
|
|
| 38 |
|
|
| 39 |
|
|
| 40 |
|
|
| 41 |
|
|
| 42 |
|
|
| 43 |
|
|
| 44 |
|
|
| 45 |
|
|
| 46 |
|
|
| 47 |
|
|
+ 35
- 0
pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/saettigung/Pizza_v1.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
+ 11
- 0
pruefungsAufgaben/P_TALS/fct1/Umkehrung_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
+ 11
- 0
pruefungsAufgaben/P_TALS/fct1/Umkehrung_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
+ 27
- 0
pruefungsAufgaben/P_TALS/fct2/analytischeGeometrie/DreiecksFlaeche_v3.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
| 26 |
|
|
| 27 |
|
|
+ 25
- 0
pruefungsAufgaben/P_TALS/fct2/analytischeGeometrie/DreiecksFlaeche_v3.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 22 |
|
|
| 23 |
|
|
| 24 |
|
|
| 25 |
|
|
BIN
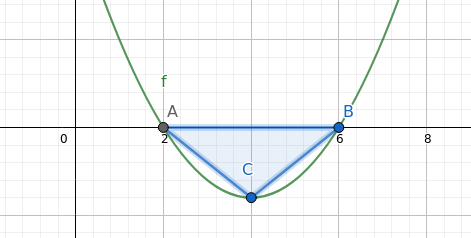
pruefungsAufgaben/P_TALS/fct2/analytischeGeometrie/img/Dreieck4_6.png
Wyświetl plik
+ 12
- 0
pruefungsAufgaben/P_TALS/fct2/findeGleichung/FindeFunktionsgleichungAusZweiPunktenUndC_TR_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
+ 12
- 0
pruefungsAufgaben/P_TALS/fct2/findeGleichung/FindeFunktionsgleichungAusZweiPunktenUndC_TR_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
+ 11
- 0
pruefungsAufgaben/P_TALS/fct2/findeGleichung/GleichungFindenAusDreiPunkten_TR_v1.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
+ 11
- 0
pruefungsAufgaben/P_TALS/fct2/findeGleichung/GleichungFindenAusDreiPunkten_TR_v1.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
+ 11
- 0
pruefungsAufgaben/P_TALS/fct2/findeGleichung/GleichungFindenAusDreiPunkten_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
+ 11
- 0
pruefungsAufgaben/P_TALS/fct2/findeGleichung/GleichungFindenAusDreiPunkten_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
+ 21
- 0
pruefungsAufgaben/P_TALS/fct2/grundlagen/WelcheSindQuadratisch_v4.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
+ 21
- 0
pruefungsAufgaben/P_TALS/fct2/grundlagen/WelcheSindQuadratisch_v4.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
+ 9
- 0
pruefungsAufgaben/P_TALS/fct2/nullstellenform/MoeglicheGleichung_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
+ 9
- 0
pruefungsAufgaben/P_TALS/fct2/nullstellenform/MoeglicheGleichung_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
+ 10
- 0
pruefungsAufgaben/P_TALS/fct2/scheitelform/GespiegelteNormalparabel_TR_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
+ 8
- 0
pruefungsAufgaben/P_TALS/fct2/scheitelform/GespiegelteNormalparabel_TR_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
+ 16
- 0
pruefungsAufgaben/P_TALS/fct2/schnittpunkt/FindeZweiSchnittpunkte_TR_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
+ 16
- 0
pruefungsAufgaben/P_TALS/fct2/schnittpunkt/FindeZweiSchnittpunkte_TR_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
+ 7
- 0
pruefungsAufgaben/P_TALS/fct2/skizzieren/ParabelSkizzieren_v2.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
+ 7
- 0
pruefungsAufgaben/P_TALS/fct2/skizzieren/ParabelSkizzieren_v2.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
+ 17
- 0
pruefungsAufgaben/P_TALS/fct2/skizzieren/Parabel_ab_charakteristischen_Punkten_v3.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
+ 16
- 0
pruefungsAufgaben/P_TALS/fct2/skizzieren/Parabel_ab_charakteristischen_Punkten_v3.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
+ 10
- 0
pruefungsAufgaben/P_TALS/fct2/transformation/GraphenTransformation_v4.tex
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
+ 10
- 0
pruefungsAufgaben/P_TALS/fct2/transformation/GraphenTransformation_v4.tex~
Wyświetl plik
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
Ładowanie…
